数组
1.存在重复元素
给定一个整数数组,判断是否存在重复元素。
如果存在一值在数组中出现至少两次,函数返回 true 。如果数组中每个元素都不相同,则返回 false 。
思路:先将数组按大小排好,利用sort(),然后在相邻之间进行比较是否要相同元素
/**
* @param {number[]} nums
* @return {boolean}
*/
var containsDuplicate = function(nums) {
nums.sort((a,b)=>b-a);
for(var i=0; i < nums.length ; i++){
if(nums[i] == nums[i+1]){
return true;
}
}
return false;
}2.最大子序和(动态规划)
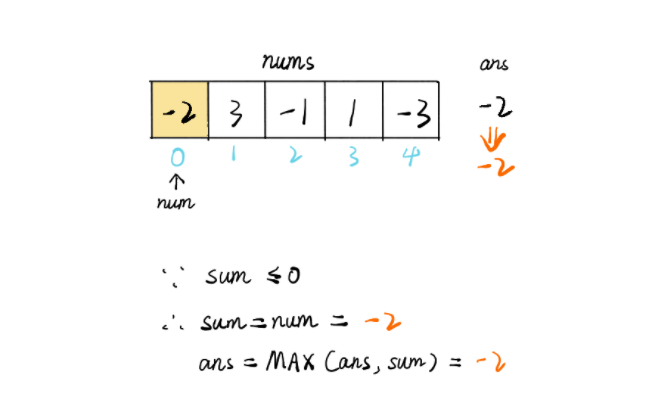
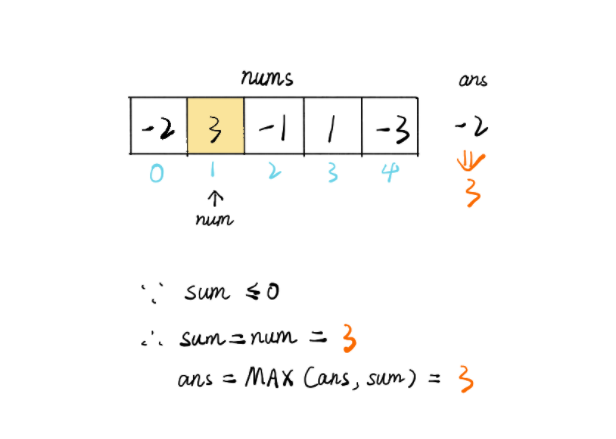
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
思路:
这种方法称作正数增益,这样子就可以找到最大的和
var maxSubArray = function(nums) {
let ans = nums[0];
let sum = 0;
for(const num of nums) {
if(sum > 0) {
sum += num;
} else {
sum = num;
}
ans = Math.max(ans, sum);
}
return ans;
};3.两数之和
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
思路:暴力解法,哈希表
/**
* @param {number[]} nums
* @param {number} target
* @return {number[]}
*/
var twoSum = function(nums, target) {
for(let i = 0;i<nums.length-1;i++){
for(let j = i+1; j < nums.length ; j++){
if(nums[i]+nums[j]==target){
return [i,j]
}
}
}
};4.合并两个有序数组
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到nums1中,使合并后的数组同样按 非递减顺序 排列。
注意:最终,合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。
思路:利用splice将sums1的替代元素删除并加上sums2
var merge = function(nums1, m, nums2, n) {
nums1.splice(m, nums1.length - m, ...nums2);
nums1.sort((a, b) => a - b);
};
方法二:双指针法
var merge = function(nums1, m, nums2, n) {
let p1 = 0, p2 = 0;
const sorted = new Array(m + n).fill(0);
var cur;
while (p1 < m || p2 < n) {
if (p1 === m) {
cur = nums2[p2++];
} else if (p2 === n) {
cur = nums1[p1++];
} else if (nums1[p1] < nums2[p2]) {
cur = nums1[p1++];
} else {
cur = nums2[p2++];
}
sorted[p1 + p2 - 1] = cur;
}
for (let i = 0; i != m + n; ++i) {
nums1[i] = sorted[i];
}
};
5.两个数组的交集
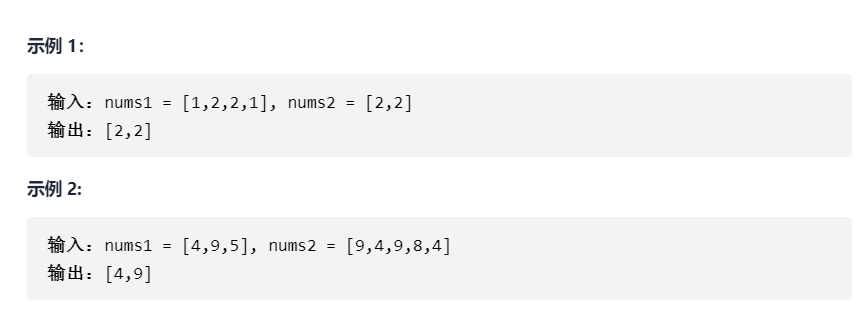
给定两个数组,编写一个函数来计算它们的交集。
思路:利用双指针进行做题
let intersect = function (nums1, nums2) {
nums1.sort((a, b) => a - b);
nums2.sort((a, b) => a - b);
let l = 0, r = 0, ans = [];
while (l < nums1.length && r < nums2.length) {
if (nums1[l] === nums2[r]) {
ans.push(nums1[l]);
l++;
r++;
} else nums1[l] < nums2[r] ? l++ : r++;
}
return ans;
};6.买卖股票的最佳时机
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
思路一:暴力解法(该方法超时了)
/**
* @param {number[]} prices
* @return {number}
*/
var maxProfit = function(prices) {
var max = 0;
for(let i = 0 ; i < prices.length-1 ; i++){
for(let j = i+1 ; j < prices.length ; j++){
const profit = prices[j] - prices[i];
if(profit > max){
max = profit;
}
}
}
if(max < 0){
return 0;
}else{
return max;
}
}思路二:贪心算法
const maxProfit = prices => {
// 先定义第一天为最低价格
let min = prices[0];
// 利润
let profit = 0;
// 遍历数据
for (let i = 1; i < prices.length; i++) {
// 如果发现比最低价格还低的,更新最低价格
min = Math.min(min, prices[i]);
// 如果发现当前利润比之前高的,更新利润
profit = Math.max(profit, prices[i] - min);
}
return profit;
};
7.重塑矩阵
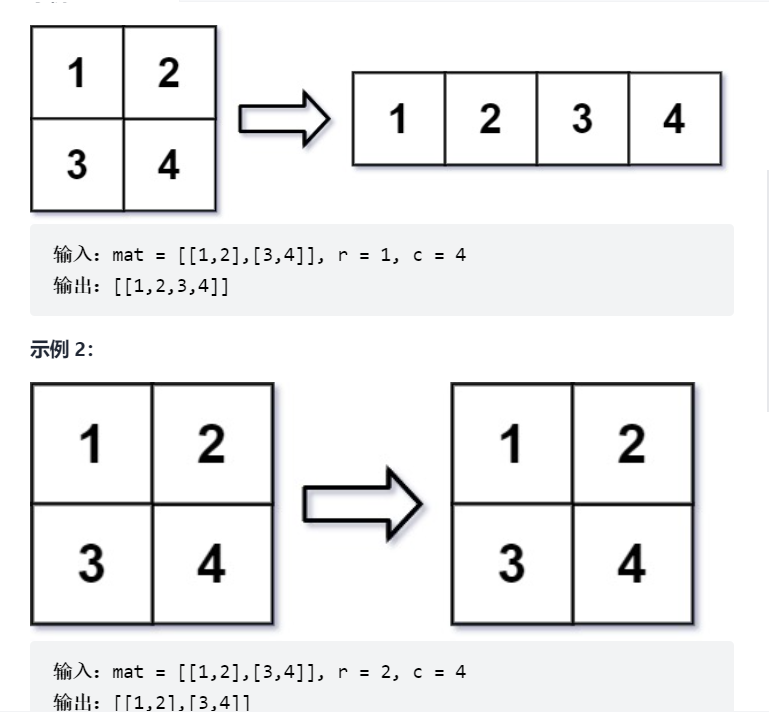
在 MATLAB 中,有一个非常有用的函数 reshape ,它可以将一个 m x n 矩阵重塑为另一个大小不同(r x c)的新矩阵,但保留其原始数据。
给你一个由二维数组 mat 表示的 m x n 矩阵,以及两个正整数 r 和 c ,分别表示想要的重构的矩阵的行数和列数。
重构后的矩阵需要将原始矩阵的所有元素以相同的 行遍历顺序 填充。
如果具有给定参数的 reshape 操作是可行且合理的,则输出新的重塑矩阵;否则,输出原始矩阵。
思路:
重塑矩阵 - 重塑矩阵 - 力扣(LeetCode) (leetcode-cn.com)
var matrixReshape = function(nums, r, c) {
const m = nums.length;
const n = nums[0].length;
if (m * n != r * c) {
return nums;
}
const ans = new Array(r).fill(0).map(() => new Array(c).fill(0));
for (let x = 0; x < m * n; ++x) {
ans[Math.floor(x / c)][x % c] = nums[Math.floor(x / n)][x % n];
}
return ans;
};
8.杨辉三角
给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。
var generate = function(numRows) {
const ret = [];
for (let i = 0; i < numRows; i++) {
const row = new Array(i + 1).fill(1);
for (let j = 1; j < row.length - 1; j++) {
row[j] = ret[i - 1][j - 1] + ret[i - 1][j];
}
ret.push(row);
}
return ret;
};9.有效的数独
请你判断一个 9x9 的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效即可。
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图)
数独部分空格内已填入了数字,空白格用 '.' 表示。
注意:
一个有效的数独(部分已被填充)不一定是可解的。
只需要根据以上规则,验证已经填入的数字是否有效即可。
const isValidSudoku = board => {
// 三个方向判重
const [rows, columns, boxes] = [{}, {}, {}];
// 遍历数独
for (let i = 0; i < 9; i++) {
for (let j = 0; j < 9; j++) {
const num = board[i][j];
if (num !== '.') {
// 子数独序号:0~8,一共9个
const boxIndex = parseInt(i / 3) * 3 + parseInt(j / 3);
// 如果当前数已经在某个位置出现过了,返回false
if (rows[i + '-' + num] || columns[j + '-' + num] || boxes[boxIndex + '-' + num]) {
return false;
}
// 三个方向上每个位置,将当前数做标记,表示出现过了
rows[i + '-' + num] = true;
columns[j + '-' + num] = true;
boxes[boxIndex + '-' + num] = true;
}
}
}
return true;
};10.矩阵置零
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
进阶:
一个直观的解决方案是使用 O(mn) 的额外空间,但这并不是一个好的解决方案。
一个简单的改进方案是使用 O(m + n) 的额外空间,但这仍然不是最好的解决方案。
你能想出一个仅使用常量空间的解决方案吗?
思路:
标记数组,我们可以用两个标记数组分别记录每一行和每一列是否有零出现。
具体地,我们首先遍历该数组一次,如果某个元素为 00,那么就将该元素所在的行和列所对应标记数组的位置置为 true。最后我们再次遍历该数组,用标记数组更新原数组即可。
var setZeroes = function(matrix) {
const m = matrix.length, n = matrix[0].length;
const row = new Array(m).fill(false);
const col = new Array(n).fill(false);
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
if (matrix[i][j] === 0) {
row[i] = col[j] = true;
}
}
}
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
if (row[i] || col[j]) {
matrix[i][j] = 0;
}
}
}
};